��3�́@POM�ɂ�����\��
�@���S�Ȏ��ƌv��i���Ɛ헪�|�o�c�헪�j�̗��Ă͓�����ł��邪�A�e�����̗\����I�m�ɍs�����ƂŐ��k���𑝂��K�v������B
�@�v��̑�1�X�e�b�v�͏����̐��i�A�T�[�r�X�A�����Ă��̎Y�ƂɕK�v�Ȏ������g�\���h���邱�ƁA�����A�g���v�\���h�Ɏn�܂�B����́APOM�ɂ����鎖�ƌv�旧�Ă̏o���_�ƂȂ�B�Ǘ��҂ɂƂ��ẮA���i�A�H�������Đݔ��ɂ��Ă̐헪�����肷�邽�߂ɁA�����Ԃɓn��\���Ƌ��ɁA2�`3�T�ԂƂ����߂������ɋN���鐻����̖��A�����A�Z���̗\�����K�v�ł���B
�@�}3.1�ɁA���ƌv��ɂ�����g�\���h�̈ʒu�t�����������B�s��̏E�o�ς̌��ʂ��E�@�K�����̃C���v�b�g���ɑ��ė\���̎�@�E���f�������p���邱�ƂŁA���v�\�����s���B���̎��v�\���͔̔��̗\�����s�������łȂ��A��ɏq�ׂ��o�c�헪�̍l�Ă�Y�ɕK�v�Ȏ����̗\���ɗp����B
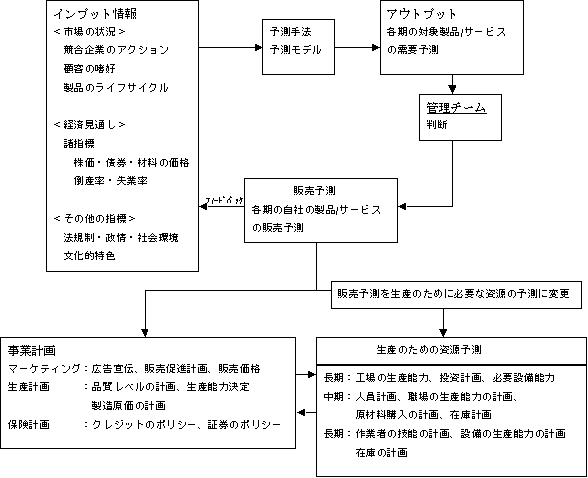 �}3.1 �o�c�v��ɂ�����\���̈ʒu�Â�
�}3.1 �o�c�v��ɂ�����\���̈ʒu�Â�
�m3�n�|1�@�\����@
�@�\����@�̃��f���ɂ́A�萫�I�Ȃ��̂ƒ�ʓI�Ȃ��̂Ƃ�����B�����ł́A���̑�\�I�Ȃ��̂������B
�m3�n�|1�|1�@�萫�I�\����@
�@�@�萫�I�ȗ\����@�͌��ʂƌ����̈��ʊW���͂����肵�Ȃ��ꍇ�ɗp��������̂ŁA�����̏o�����ɑ��钼���I�Ȕ��f���܂�ł���B
�@��Ƃ̖�����iExecutive�@Committee�j�̈ӌ���f���t�@�C�@�́A�̔��\����V�������i/�T�[�r�X�͂��Ƃ�茻�݂̐��i/�T�[�r�X�̗��҂ɂ��ċ��ʂ̌������������߂ɗp������B����A�w���͒�����ڋq�i����ҁj�����͖{���I�ɂ͌����̐��i�ɑ��ĉ��p������@�ł���A����ɑ��A���j�I�ȗގ����̕��͂�s�꒲���͐V���i/�T�[�r�X�Ɋւ�����悤�Ƃ���l�ɉ��p�����B
�@
�m3�n�|1�|2�@��ʓI�\����@
�@�@��ʓI�\����@�Ƃ́A�ߋ��̃f�[�^�Ɋ�Â������w�I��@�ł���A�ߋ��̎��ۂ����ꂩ��N����Ɨ\������鎖�ۂƗގ����Ă���ł��낤�Ƃ̉���Ɋ�Â��Ă���B�ʏ킢�����̗ǂ��������ۂ���������̂ł��邪�A���̗\���̐��m���i���x�j����������K�v������ƂƂ��ɁA�\�����x�������ꍇ�͗\�����f����@�̕ύX���s���K�v������B��ʓI�\����@�̑�\�I�ȗ�����Ɏ����B
1.�@���`��A
�ŏ�2��@�ƌĂ����@��p���ĖړI����1���邢�͕����̓Ɨ��ϐ��̊W���`���A���n��̊W��\������B�P��A���͂ɂ����ēƗ��ϐ���1�ł���A�d��A���͂ɂ����Ă͕����̓Ɨ��ϐ���p����B�����A���n��f�[�^�����Ԃ̂悤�ȘA���ł�����̂̏ꍇ�́A�Ɨ��ϐ��ɂ͊��Ԃ�p���A�ړI���͎��v�ƂȂ�B���`��A�͕��ʁA�����\���ɗp�����邪�A�����̕����̊��Ԃ����ɑ���Z���\���̎�@�Ƃ��Ă����p�ł���B
2.�@�ړ����ϖ@
�����̎��v��\������Z���\�����f����1�ł���B���̕��@�͍ŋ߂̖��m�ȃf�[�^����Z�p���ς��o���A���̒l�������̗\���ɗp������̂ł���B
3.�@�d�ݕt���ړ����ϖ@
���̃��f���͈ړ����ϖ@�̎Z�p���ς̑���Ɋ��ɑ���d�ݕt�����ς�p���Ď����̗\�����s�����̂ł���B
4.�@�w�������@
�Z���̎��v��\��������̂ŁA���̕��@�͎��v�\���l�����̊��Ԃ̗\���G���[���l���ɓ���ďC��������̂ŁA�C���\���������̗\���ɗp����B�@
5.�@�g�����h���l�������w�������@
�w���������f���̏C���Ƀg�����h�̃p�^�[�������������̂ł���B���̕��@�͏d�w�������@�ƌĂ�A���ς̗\���ƃg�����h�̗\�����ɍs����B
�m3�n�|2 �����\��
�@�����\���Ƃ́A�����̂���1�N�ȏ�̊��Ԃ̗̏\�����s�����Ƃł���B�����\���͐��i�A�H���A�e�N�m���W�A�v�ɂ��Ă̐헪�I������s��POM�ɕs���Ȃ��̂ł���B
�@���Y�V�X�e���̒����I�Ȑ����ɂƂ��ė\�����ʂ��d�v�ƂȂ邢�����̗��������Ǝ��̗l�ɂȂ�B
�@ �V���i�̐v�ɍۂ�
�@ ���v�\���ɂ�萶�Y���ʂ����Ȃ�̗ʂł���A�����������݂������ǂ��Ɣ��f��
�ꂽ�Ȃ�A���i�v���猩�����K�v�����낤�B
�A �V���i�̐��Y�ʂ̌���ɍۂ�
�@ �ǂ̂��炢�̗ʂ��K�v�Ƃ���邩�̏�����ɁA�ǂ̂��炢�̋K�͂̐ݔ����K�v
���̌����A�܂��A�ǂ��ɂ���𗧒n�����邩�̌���
�B �������B�̌v�旧�Ăɍۂ�
�@ �\���̓}�l�[�W���[�����������̒����I�Ȍ_������Ԕ��f�ƂȂ�B�����\���͐V
�����@�B�̍w���⌚���̌��݁A���ޗ��̒��B��̊J���Ƃ�����������i�W������B
�@�����\���̃f�[�^�̒��ɂ͐}3.2�Ɏ����悤�Ȃ������̌X���������Ă�����̂�����B����̓g�����h�ƌĂ��㏸�A���~�X���A�������A�G�ߐ��Ȃǂł���A�����̌X���������Ȃ��ꍇ�������_�����邢�́A�m�C�Y�ƌ����B
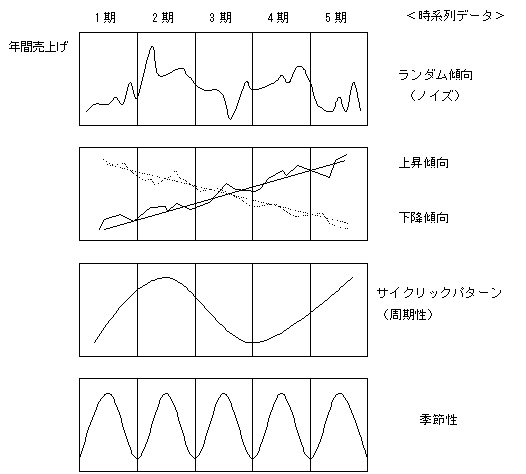
�@�@�@�@�@�@�@�@�@�@�}3.2 ���n��f�[�^�Ɋ܂܂��g�X���h
�m3�n�|3�@���`��A�Ƒ��֊W
�@���炩�ȌX��������ꍇ�͎��n��f�[�^�𐳊m�ɃO���t�����\���ɗp���邱�Ƃ��ł��邪�A���m�ɃO���t���ł��Ȃ��ꍇ�ɗp������@�Ƃ��ĉ�A���͂�����B
�@���`��A���͂�1�̖ړI�ϐ���1���邢�͕����̓Ɨ��ϐ��Ƃ̊W��\�����\�����f���ł���B����������ɂ͖ړI���̒l��\�����邽�߂̓Ɨ��ϐ��̒l�Ƃ����̊W�ɂ��čl���Ȃ���Ȃ�Ȃ��B
�@�\3.1�͕ϐ��A�ϐ��̒�`�A�P��A���͂̎������������̂ł���B���̃��f����Y=a+bX�̌`�ŁA��A�������ƌĂ�Ă���B���̎��ł́AY���ړI�ϐ��ŗ\���l�ł���AX�͓Ɨ��ϐ��ƂȂ�B������a��y�i��j�ؕЂ�,b�����A�W���ƌĂ�Ă���B�\3.1�̕�������p���邱�ƂŁA����a��b�͌v�Z�ł���B
�\3.1 �ϐ���`�ƒP��A���͂̕�����
�@�@x�F�Ɨ��ϐ��@�@�@�@�@�@�@�@�@Y�FY=a+bX���y�̒l
�@�@y�F�ړI�ϐ��@�@�@�@�@ �@ X�FY=a+bX���x�̒l
�@�@n�F�ϑ����@�@�@�@�@�@�@�@�@�@r�F���W��
�@a�F��ؕЁ@�@�@�@�@�@�@�@�@�@r2�F��^��
�@�@b�F���A�W��
�@�@y�F�ړI�ϐ��̕��ϒl
Y = a + bX ![]()
�@�@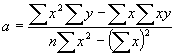 �@�@�@
�@�@�@
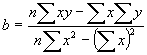
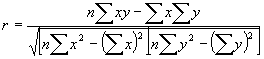
�@�P��A���͓͂Ɨ��ϐ������ԈȊO�̕ϐ��̏ꍇ�ɂ��g�p�ł���B���̂悤�ȏꍇ�ɂ́A�P��A���͂͋����I�\�����f���iCausal forecasting model�j�ƌĂ��\�����f���̒���1�Ƃ��Ĉʒu�t������B�����̃��f���͖ړI�ϐ���1�������͕����̓Ɨ��ϐ��Ƃ̊֘A���𑪂�����A�m�������肷��ۂ̗\���Ƃ��Ĕ��W���Ă���B���̎�̃��f���͔���̓]�@��\������̂ɗD��Ă���B
�@���W��(r)�Ƃ�y��x�̑��֊W�̏d�v�x�ł���
�@r�Ƃ����W���́|1����{1�̐��l���Ƃ萳���͊W�̕�������\����܂����l�̐�Βl�͊W�̋�����\���Ă��顁@r��b�̕����͏�ɓ����ł��顕���r��y��x�̒l�����̕����֤����r��y��x�̒l�����������ֈڍs���Ă������Ƃ�\���Ă��顈ȉ��Ɋ����r�̒l�̈Ӗ���\���
�|1:���S�ȕ��̊W y���㏸����ɘA���x�����~���顂܂�y�����~�Ȃ�x��
�@�@�@�@�㏸�ł���
�{1:���S�Ȑ��̊W y���㏸����ɘA���x���㏸���顂܂�y�����~�Ȃ�x��
�@�@�@���~�ł���
�@�@0: y��x�ɂ͊W���Ȃ��

�@���W����x��y�̊W�𐔒l������ۂɖ𗧂��������K�x��ア��Ƃ��������t�͊W��\���ɂ͓I�m�ȕ\���Ƃ͌����Ȃ����낤�����W���ł���r2�͑��W��r���悵�����̂ł���Ar����r2�ւ̕ω��́A�W�̐��l������ϓI�Ȃ��̂��礂�薾�m�Ȃ��̂ւ��邱�Ƃ��o���顁@y�̕ω��ʂɂ͎���3��ނ����݂���
�S�̂̕ω����͑S�Ă�y�̒l���炻�̕��ϒl�ł���y�����������̂̓��̍��v��
����
�@�����̂��ω����̓g�����h���C�����Y����y�����������̂̓��̍��v�ł���
�@�����̂��Ȃ��ω���(�����_���Œ�`�ł��Ȃ���)�ͤy����g�����h���C�����Y
�@�����������̂̓��̍��v�ł���
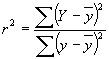
![]()
�@����W���͐����̂��ω��ʂ��S�̂̕ω��ʂ̒��Ő�߂Ă��銄���Ō��܂�A����
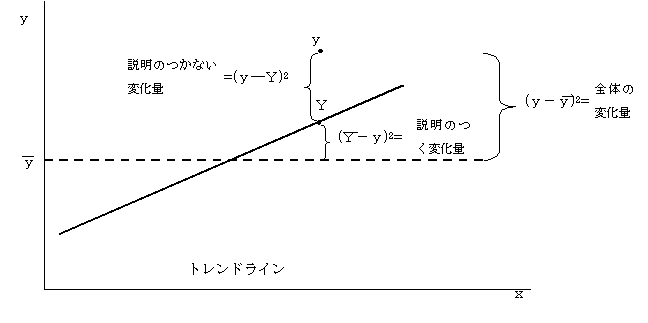
�]���Č���W���ͤ�]���ϐ��ł���y�ŕ\�����S�̂̕ω��ʂ��A�ǂ̒��xx��g�����h���C���ɂ���Đ����������Ƃ������Ƃ�\���Ă���
����W��r2=80%�Ƃ́A���グ���Ɨ��ϐ�(y)��80%��������Ă��鎖�������Ă���B�����c���20����x�ȊO�̕ϐ����邢�͋��R������߂Ă���Ɣ��f�ł���B�������W���ƌ���W���͓Ɨ��ϐ��Ə]���ϐ��̒l�̊֘A�x�𑪒肷��̂ɖ��ɗ��¡�֘A���������قǂ��̕����������萳�m�ȗ\���𗧂Ă邱�Ƃ��\�ł��顂������P��A���͂ɂ���͈͂����Ɨ��ϐ���1�ł��邪���߂ɕ��G�Ȍ����̐��E�̖��A���Ƀr�W�l�X����̗l�ɍ������m�������߂���\���ɂ͌��E�����顂����ŕ����̓Ɨ��ϐ��ɂ���Ă�萸�x�̍����\�����s�Ȃ����߂ɏd��A���͂��s�Ȃ���B�Ⴆ�A�����̔��グ�iY�j�͍����̉ݕ��̐ωׁiX1�j����S�l���iX4�j��4�̓Ɨ��ϐ����玦�����B
![]()
Y=�����̔���グ(�S���~)
X1=�O���̍����̉ݕ��ω�(�S��)
X2=GNP�̐�����(%*�ꖜ)
X3=�n���̎��Ɨ�(%*�ꖜ)
X4=�S�l��(��l)
�l�����͒P��A���͂�Y=a+bX�Ɠ��l�ł��邪����ӂ��ׂ��_��X���O���̐��l�ł���Ƃ������Ƃł��顂��̂悤��X��O�����ĕ������Ă��鎖����旧�w�W�ileading indicator�j�ƌĂԡ�\�����s���Ƃ��ɂͤ���̗l�Ȑ旧�w�W����Ɍ��o�����Ƃ��]�܂�������̂Ȃ�Ɨ��ϐ�X�̌��ς�����s���K�v���Ȃ�����ł���
�����ł͈���Ȃ����A����^�d��A����,Stepwise
Regression,�������W��,�d���W���Ȃǂ��\���̕��͎�@�Ƃ��Ēm���Ă���B���@�ׂȎ�@�ł��邪��{�I�T�O�͓��l�̂��̂ł���B
�m3�n�|3�|3 �덷�͈̗̔͂\��
�@�덷�P��A���͂͏����̌��ς�����s�����̂ŏ�Ɍ덷��������\�������顏]���ė\���������������I�ȕω��ʂɒ��ʂ��邱�Ƃ͗ǂ����邱�Ƃł��題덷�͈̗͂\���͉ߋ��̃f�[�^����N���蓾��͈͂�ݒ肷�邱�Ƃɂ���āA�s���m�ȗ\������͂��邱�Ƃ��ł����@�ł���B�܂菫���N���肻���Ȏ���\���̒��Ɋ܂ޗl�ȋ����I�v����s�Ȃ��A���M���������߂邱�Ƃ�ړI�Ƃ��Ă���B���͈̔͗\���ɂ���āA�_��ȑΉ����\�ɂȂ�B
�\���̕W���I�덷�i���\���̕W�����j�FSyx
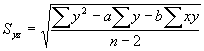
�덷�̏���FUL�A�����FLL�͎����ŗ^������B
UL
(Upper Limit) = Y + t�ESyx
LL (Lower Limit) = Y - t�ESyx
�m3�n�|3�|2�@�G�ߕϓ��̗\��
�@�G�ߕϓ��̃p�^�[���͕��ʈ�N�̊ԂɋN���褂����Ė��N���̌X�����J��Ԃ���顂����̋G�ߕϓ��͓V��x�����������s���Ȃǂɂ���Ĉ�����������顗\�ߌ����ƕϓ��̃p�^�[�����𖾂���Ă��邽�߁A���ۂɗ\�����s�Ȃ����͂��̃p�^�[���Ă͂߂�B
�i��1�j�@�G�ߕϓ����l�����\��
�@�����H�Ƃ̍�������͗��N�̊e�l�����̎����A�l���A�y�ь��ޗ��ƕK�v���Y�ʂ̎Z�o�����݂����B�ߋ��R�N�Ԃ̊e�l�������Ƃ̔���f�[�^����A���N����͓����悤�ȋG�ߕϓ������Ă���A���N�������Ȃ�ł��낤�ƍl������B�������������N�̔����\���ł���A�ړI�Ƃ���K�v�Ȏ����A�l���A�y�ь��ޗ��Ɛ��Y�ʂ�����ł���ƍl������B
�P.�@�ߋ��̔����������B
|
|
|
�l�������Ƃ̔���i�P�ʁF��j |
|
|||
|
|
�N�� |
Q1 |
Q2 |
Q3 |
Q4 |
���v |
|
|
8 |
320 |
630 |
500 |
620 |
2,070 |
|
|
9 |
280 |
720 |
520 |
480 |
2,000 |
|
|
10 |
380 |
800 |
440 |
540 |
2,160 |
|
���v |
|
980 |
2,150 |
1,460 |
1,640 |
6,230 |
|
���� |
|
326 |
716 |
486 |
546 |
519* |
|
�G�ߎw���iS.I.�j* |
0.629 |
1.381 |
0.938 |
1.053 |
|
|
*�FS.I. = �i�l�������Ƃ̕��ρj�^�i�S�̂̕��ρj���i�l�������Ƃ̕��ρj�^519
2.�@S.I.�i�G�ߎw���j�Ŋe�l�����̃f�[�^�������ċG�ߕϓ����Ȃ����B
�@�@�Ⴆ�A320��0.629��508.7�A630��1.381��456.2�ȂǁB
|
|
�G�ߕϓ����Ȃ������l�������Ƃ̐��l |
|||
|
�N�� |
Q1 |
Q2 |
Q3 |
Q4 |
|
8 |
508.7 |
456.2 |
533.0 |
588.8 |
|
9 |
445.2 |
521.4 |
554.4 |
455.8 |
|
10 |
604.1 |
579.3 |
469.1 |
512.8 |
3.�@�G�ߕϓ����Ȃ������f�[�^�i�S12�l�����j��p���ĉ�A���͂��s���A���N�̊e�l�����̗\��������B
|
���� |
X |
y |
Y2 |
X2 |
xy |
|
8�N��Q1 |
1 |
508.7 |
258,775.69 |
1 |
508.7 |
|
8�N��Q2 |
2 |
456.2 |
208,118.44 |
4 |
912.4 |
|
8�N��Q3 |
3 |
533 |
284,089 |
9 |
1,599 |
|
8�N��Q4 |
4 |
588.8 |
346,685.44 |
16 |
2,355.2 |
|
9�N��Q1 |
5 |
445.2 |
198,203.04 |
25 |
2,226 |
|
9�N��Q2 |
6 |
521.4 |
271,857.96 |
36 |
3,128.4 |
|
9�N��Q3 |
7 |
554.4 |
307,359.36 |
49 |
3,880.8 |
|
9�N��Q4 |
8 |
455.8 |
207,753.64 |
64 |
3,646.4 |
|
10�N��Q1 |
9 |
604.1 |
364,936.81 |
81 |
5,436.9 |
|
10�N��Q2 |
10 |
579.3 |
335,588.49 |
100 |
5,793 |
|
10�N��Q3 |
11 |
469.1 |
220,054.81 |
121 |
5,160.1 |
|
10�N��Q4 |
12 |
512.8 |
262,963.84 |
144 |
6,153.6 |
|
���v |
��x=78 |
��y=6,228.8 |
��y2=3,266,386.52 |
��x2=650 |
��xy=40,800.5 |
4.�@������p���ė\�������쐬����B
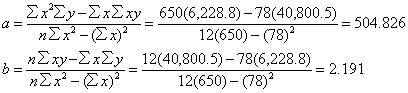
Y=a+bX=504.826+2.191X
5.�@�w�ɗ��N�̊e�l�����̒l�ł���13�C14�C15�C16��������B��������Z�o�����l�́A
�@�@�G�ߕϓ����Ȃ��������N�̊e�l�����̗\���l�ł���i�P�ʂ͐�j�B
�@�@Y13=504.826+2.191 (13)=533.309
Y14=504.826+2.191 (14)=535.5
Y15=504.826+2.191 (15)=537.691
Y16=504.826+2.191 (16)=539.882
�U.�@�G�ߎw���iS.I.�j���g���ċG�ߕϓ��̂���\���l���Z�o����B
|
�l���� |
S.I. |
�G�ߕϓ��̂Ȃ��\���l |
�G�ߕϓ��̂���\���l |
|
Q1 |
0.629 |
533.309 |
335 |
|
Q2 |
1.381 |
535.5 |
739 |
|
Q3 |
0.938 |
537.691 |
504 |
|
Q4 |
1.053 |
539.882 |
568 |
�m3�n�|4�@�Z���\���ƃp�t�H�[�}���X�̕]��
�@�Z���\���͈�ʂɐ������琔�T�Ԃ̃^�C���X�p���ŏ����̏�Ԃ�\������ۂɎg����B�Z���Ԃ䂦�A�������A�G�ߕϓ��A�g�����h�p�^�[���̉e�����邱�ƂȂ������_���ȕϓ��i�m�C�Y�j�͑ΏۂƂ���B���̒Z���\������A�����i�����A���T���j�̐��Y�i�ڋy�ѐ��Y���ʁA����ɔ������ޗ��̒��B�ʂ̌���B�K�v�ȍH���̌��ς蓙���s����B
�Z���\�����f���̃p�t�H�[�}���X�̕]����Impulse Response�A�m�C�Y�ɏՐ��A���x�Ƃ����R�̊ϓ_����]�������B���̓��e�����Ɏ����
�EImpulse Response�ƃm�C�Y�ɏՐ�
�@��ɏq�ׂ��悤�ɒZ���\���ł́A�����_���ȕϓ��A�������̓m�C�Y������B�����\���l�ɂقƂ�ǃ����_���ϓ����܂܂�Ă��Ȃ��Ȃ�A���̗\���l�̓m�C�Y�ɏՐ��������ƌ����B�܂��ߋ��̃f�[�^�̉e����q���Ɏ�\���̂��Ƃ�Impulse Response�������ƕ\������B�Z���\���ɂ������āA��ʂɂ�Impulse Response�y�уm�C�Y�ɏՐ��������ق����]�܂������A�f�[�^�̕ω��̉e�����₷���Z���V�e�B�u�ȗ\���V�X�e���Ƃ͕K�����ɑ����̃m�C�Y���E�����̂䂦�A���̗l�Ȏ��͂܂����肦�Ȃ��B���������ė\���҂�Impulse Response���������A�������̓m�C�Y�ɏՐ����������A�����ꂩ���ʂ̍����Ǝv�������I�Ȃ���Ȃ�Ȃ��̂ł���B
�E�\�����x�̑���
�@�\�����f���̐��x�́A���ۂ̐��l���\���l�ɂǂꂾ���߂����̕]���ɂ�邪�A�ʏ펟��3�̕��@���g����B
�i�P�j�\���l�̕W�����[(Syx)
�i�Q�j����MSE(Mean Squared Error�iSyx)2�j

�i�R�j�\���l�Ǝ��ђl�̍��̐�Βl�̕��ρiMAD�FMean Absolute Deviation�j
�\���덷������͈͂Ȃ�AMAD��Syx�Ƃ̊W�͎��̂悤�ɕ\�����B
Syx=1.25MAD
MAD,Syx��MSE�͒����A�y�ђZ���\�����f���̗\����̐��x�𑪒肷�邽�߂Ɏg����B���AMAD�͒Z���\�����f�����쐬����ۂ֗̕��ȕ]���w�W�Ƃ��Ă����p�����B
�@�������A�Z���\���̑�\�I�Ȏ�@�������B
�m3�n�|5�@�ړ����ϖ@
�ړ����ϖ@�́A�ŋ߂̂������̃f�[�^�ς��āA��������̗\���l�Ƃ��Ďg�p������@�ł���B���̗�ł́A�ړ����ϖ@�̎��ۂ�������Ă���B
�i��2�j�@�ړ����ς�p�����Z���\��
�ɊǗ��҂̏��т́A�e�T�ɂ�����q�ɂ���̍ɗ��o�ʂ����ς���Z���\���V�X�e������낤�Ǝv�����B�ɂ̎��v�ʂ͐��T���ƂɃ����_���ɕϓ����Ă��邪�C�S�̂ł͈��肵�Đ��ڂ��Ă���B��Ђ̖{�����炫���A�i���X�g�́A3�C5��������7�T���Ƃ̈ړ����ς��Ƃ�悤��Ă����B���̂����̈���̗p����O�ɁA�ߋ�10�T�Ԃ̗\�������Ă݂邱�Ƃł��ꂼ��̐��x���r���悤�ƍl�����B
�P.�@3,5,7�T���Ƃ̈ړ����ς��v�Z����B
|
|
�����l |
|
�\���l |
|
|
�T |
�i�P�ʁF��h���j |
AP=3�T�� |
AP=5�T�� |
AP=7�T�� |
|
1 |
100 |
|
|
|
|
2 |
125 |
|
|
|
|
3 |
90 |
|
|
|
|
4 |
110 |
|
|
|
|
5 |
105 |
|
|
|
|
6 |
130 |
|
|
|
|
7 |
85 |
|
|
|
|
8 |
102 |
106.7 |
104.0 |
106.4 |
|
9 |
110 |
105.7 |
106.4 |
106.7 |
|
10 |
90 |
99.0 |
106.4 |
104.6 |
|
11 |
105 |
100.7 |
103.4 |
104.6 |
|
12 |
95 |
101.7 |
98.4 |
103.9 |
|
13 |
115 |
96.7 |
100.4 |
102.4 |
|
14 |
120 |
105.0 |
103.0 |
100.3 |
|
15 |
80 |
110.0 |
105.0 |
105.3 |
|
16 |
95 |
205.0 |
103.0 |
102.1 |
|
17 |
100 |
98.3 |
101.0 |
100.0 |
�\���l�͌��̃f�[�^�ɔ�ׁA���鐔�𒆐S�ɕϓ����邱�Ƃɒ��ӁB
�@�v�Z��\�\��10�T�̗\��
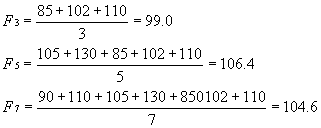
���F��10�T�ڂ̗\���l�����߂�̂ɑ�10�T�ڂ̎����l�͊܂߂Ȃ��B
�Q.�@�eAP�ɑ���\���l�Ǝ����l�Ƃ̍��̐�Βl�̕��ρiMAD:Mean Absolute
�@�@Deviation�j�����߂�B
|
|
|
�\���l |
|||||
|
|
�����l |
AP=3�T�� |
AP=5�T�� |
AP=7�T�� |
|||
|
�T |
�i�P�ʁF��h���j |
�\���l |
�� |
�\���l |
�� |
�\���l |
�� |
|
8 |
102 |
106.7 |
4.7 |
104.0 |
2.0 |
106.4 |
4.4 |
|
9 |
110 |
105.7 |
4.3 |
106.4 |
3.6 |
106.7 |
3.3 |
|
10 |
90 |
99.0 |
9.0 |
106.4 |
16.4 |
104.6 |
14.6 |
|
11 |
105 |
100.7 |
4.3 |
103.4 |
1.6 |
104.6 |
0.4 |
|
12 |
95 |
101.7 |
6.7 |
98.4 |
3.4 |
103.9 |
8.9 |
|
13 |
115 |
96.7 |
18.3 |
100.4 |
14.6 |
102.4 |
12.6 |
|
14 |
120 |
105.0 |
15.0 |
103.0 |
17.0 |
100.3 |
19.7 |
|
15 |
80 |
110.0 |
30.0 |
105.0 |
25.0 |
105.3 |
25.3 |
|
16 |
95 |
105.0 |
10.0 |
103.0 |
8.0 |
102.1 |
7.1 |
|
17 |
100 |
98.3 |
1.7 |
101.0 |
1.0 |
100.0 |
0 |
|
���̍��v |
|
104.0 |
|
92.6 |
|
96.3 |
|
|
���̕��ϒl�iMAD�j |
|
10.40 |
|
9.26 |
|
9.63 |
|
�R.�@AP=5�̏ꍇ��MAD���ŏ��ł���̂ŁAAP=5�̎��ɍł����x�������ƍl������B
�@�@AP=7�̏ꍇ��MAD��AP=5�̏ꍇ�ɔ�ׂĂقƂ�Ǎ����Ȃ��̂ŁA���������T��
�@�@�v�����𑝂₵�čl���Ă��ǂ���������Ȃ��B
�S.�@AP=5�Ƃ���18�T�ڂ̕K�v�ʂ��v�Z����B
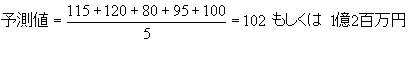
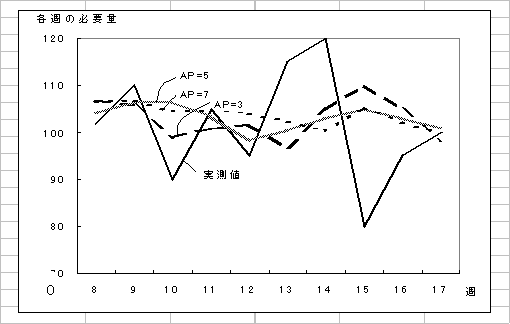
�}3.3�@��2�ł̎����l�Ɨ\���l�Ƃ̔�r
�}3.3�͗�2�̎����l�ɑ���3�̈ړ�����AP=3,5,7�T�̗\�����ł���BAP���傫���قǃm�C�Y�ɏՐ��������A�m�C�Y�̉e�����ɂ����BAP=7�̗\���l�̃O���t�͊��Ԃ��Ƃ̉e��������قӂǔ��f���Ă��Ȃ����ߑ���2�ɔ�ׂĊ��炩�ŁA�m�C�Y��ǂ��}���A�e�������܂�Ă��Ȃ��BAP�̑I���́A�]�ސ��x�̊�AImpulse Response�A�m�C�Y�ɏՐ��Ɉˑ����A�����I�ɋ��߂Ȃ��Ă͂Ȃ�Ȃ��B
�m3�n�|6�@���d�ړ����ϖ@
�ߋ��̃f�[�^�ɋϓ��ɏd�ݕt�����s�Ȃ������̂��ړ����ϖ@�ł������̂ɑ��A���n��̃f�[�^���V�����Ȃ�قǗ\���l�̉e�����傫���Ȃ�ꍇ�́A�s�ϓ��ɏd�ݕt�������������]�܂����B
|
|
�����l |
���d�i�E�F�C�g�j |
|
��V�T |
50 |
0.20 |
|
��W�T |
60 |
0.30 |
|
��X�T |
66 |
0.50 |
�\���l Y10 = 0.2(50)+0.3(60)+0.5(66) = 61
�@�w�������@
�w�������@���s�����߂̕ϐ��A�ϐ��̒�`�y�ь������\3.2�Ɏ�����Ă���B�w�������@�́A�O�̗\���l�Ǝ��ђl�̌덷��0�`1�͈̔͂ŗ^�����������W���i���j���|���邱�Ƃœ�����������O���̗\���l�ɑ������ƂŎ����̗\���l�悤�Ƃ�����̂ł���B
�\3.2�@�w�������@�̕ϐ��̒�`�ƌ���
![]()

![]()
![]()
![]()
�i��3�j�@�w�������@�ɂ��Z���\��
�@���̃f�[�^����T���Ƃ̑q�Ɏ��v�ɂ�\���������
![]() �@�����萔 =0.1, 0.2, 0.3�Ƃ�10�T��̗\��������
�@�����萔 =0.1, 0.2, 0.3�Ƃ�10�T��̗\��������
�P�D
![]() �@�@�@�@�@�@�@�@�@�@�@��p���Čv�Z������n=�T�A=���f�[�^�F=�\���l
�@�@�@�@�@�@�@�@�@�@�@��p���Čv�Z������n=�T�A=���f�[�^�F=�\���l
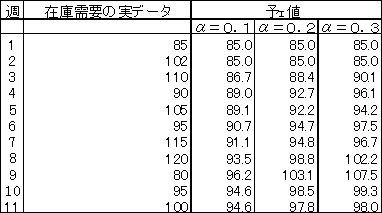
2.�@���f�[�^�Ɨ\���l�̍����Ƃ�=��Ό덷
��Ύw���̕��ς�����=���ϐ�Ό덷
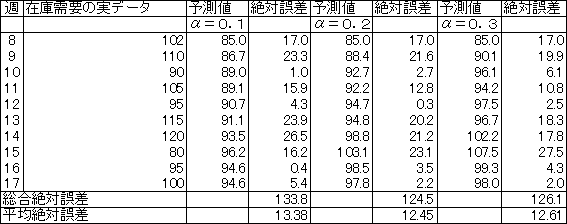
3.�@���ϐ�Ό덷�������Ƃ����������̂�I�����顂��̏ꍇ� �� =0.2
![]() 4.�@�@=0.2�Ƃ���18�T�̗\�����v�����߂�
4.�@�@=0.2�Ƃ���18�T�̗\�����v�����߂�
F18=F17+0.2*(��17-f17)=97.8+0.2*(100-97.8)=98.2��������98,200
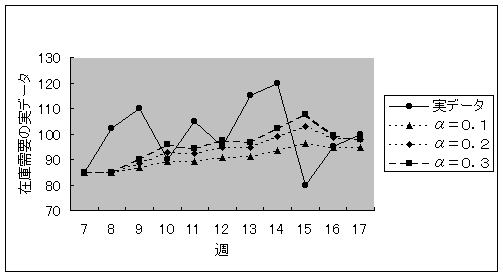
�}3.4 �����萔���Ɨ\��
![]() �}3.4���� �̒l�������Ƃ����x����\�����o����Ƃ͌���Ȃ����������I�����̒l�����߂Ȃ���Ȃ�Ȃ��B
�}3.4���� �̒l�������Ƃ����x����\�����o����Ƃ͌���Ȃ����������I�����̒l�����߂Ȃ���Ȃ�Ȃ��B