4.3　VRPの基礎

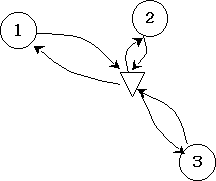
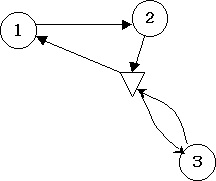
現在、企業の経営においてコスト削減は非常に重要である。 しかし、製造コスト削減が難しくなった今、物流コスト削減が非常に注目を浴びている。 　企業が物流を行うにあたり重要なことは、物流費の多くを占める配送コスト を最小化する配車計画を実現することである。 これはVRP（Vehicle Routing Problem）として様々な状況に応じた 数多くの研究がなされており、ソフトウェアも開発され、利用されている。 　このVRPの核となるのが、TSP(Traveling Salesman Problem＝巡回セールスマン問題） に現実的な前提条件を加えて配送経路問題としたClassical VRPである。 ここではその現実的な前提条件を示す。 (固定された前提条件) 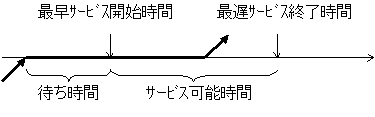各トラックは出発したDepotに必ず戻る 各需要地は必ず一台のトラックから配送される 各トラックは必ず複数の需要地に配送可能である 全需要地は需要量分必ず配送される 各トラックの積載量には制限がある (変更の対象とされる前提条件) 配送センター(デポ)の数 ：一つ、複数 需要量の性質：確定的、確率的 ビークルの種類：一種類、複数種類 時間制約： 有り、無し 1ビークルあたりのルート数：一つ、複数 　また、上述の時間制約のことをTIME WINDOWと呼ぶ。 TIME WINDOW とは、顧客側に指定された配送可能な時間の幅のことを言う。 運搬業者はこれらのTIME WINDOWに対し決められた 運搬最早時間と最遅時間を守りながら、 最適な運搬ルートと運搬時刻を決定しなければならない。 このようなTIME WINDOWか先行順序関係が与えられた場合、 それは経路決定とスケジューリングの融合問題 （Vehicle Routing and Scheduling Problem）である。 経路は総運搬コストを最小にするために設計されるが、 同時にスケジューリングが実行可能であることが保証されなければならない。 　最も理想的なのは最適解を求めることであるが、需要地数が増えると 計算時間が膨大にかかってしまい、現実的ではない。 そこで、これらのソフトウェアのほとんどはヒューリスティック技法（近似解法） を用いている。このヒューリスティック技法を用いることにより、現実的な時間で ある程度良い解を出すことができる。 　ここではまず、一般的なヒューリスティック技法の一つである セービング法についてのアルゴリズムを、 その次にTimeWindowを持つ問題に適した技法であるグリーディー法を説明する。

1964年にClark＆Wrightによって提案されたセービング法は、 数多いヒューリスティック技法の原点と言える。 この技法は、2需要地に対するピストン輸送をルート輸送に変えることによって生じる 走行距離の減少分であるセービング値を算出し、 これが最大となるルートの結合を行うことによって解を構築していく技法である。 以下にセービング法のアルゴリズムを示す。 《セービング法のアルゴリズム》 STEP1： すべての需要地と供給地間でピストン輸送を考え、初期解とする。 STEP2： 供給地と結合している需要地すべての結合の組み合わせについてセービング値を算出する。 (供給地と結合していない需要地同士を結合してしまうとルートの中に閉ループが発生してしまうため、 これらについては考慮しない。) この時、結合により積載可能量などの制約条件を超えてしまう場合には、セービング値を０とする。 STEP3： ０を超えるセービング値が存在する場合には、それが最大となる結合を行い、STEP2に戻る。 もし、すべてのセービング値が0以下である場合には、現ルートが最終ルートとなる。 計算例 STEP1： 　ピストン輸送で初期ルートを生成。 各需要地間の距離・需要量 Depot １ ２ ３ 需要量 Depot 0 30 10 20 １ 30 0 15 45 5 ２ 10 15 0 25 20 ３ 20 45 25 0 10 　　トラック積載制限：30 　　トラック走行制限：100 STEP2： 　セービング値の算出 D-1-2-D　(30*2+10*2)-(30+15+10)=25 D-2-3-D　(10*2+20*2)-(10+25+20)= 5 D-1-3-D　(30*2+20*2)-(30+45+20)= 5 トラックの積載制限・走行制限の範囲の距離で、セービング値が最大である D-1-2-Dのルートを作成する。 STEP3： 　トラックの積載制限からこれ以上の需要地を取りこむことはできないので終了。

ある需要地の最遅サービス時間から現在の時間を引いたものと 現在の場所からその需要地までの距離をそれぞれ重み付けした和が最小である需要地を 次に訪れる需要地として選択する。 ここでトラックの積載可能量または走行可能距離を超えた場合は倉庫に帰り、 また新たなルートを構築する。 目的関数　　Min{α(移動距離)＋β(余裕時間)}

※移動距離：現在の場所から次の需要地までの距離 　余裕時間＝最遅サービス時間−現在の時間（荷卸が終了した時間） 　最遅サービス時間＝最遅時間−荷卸時間

---