Excelソルバーによるロジスティクス最適化

　前回は、Excelを用いたシミュレーション上でビールゲームを行うことによって、発注方法の変更がゲームの「成績」に どう影響するかを調べました。シミュレーションは、定められた意思決定の方法にしたがって、システムを運用した ときにいかなる結果となるかを分析する、手軽かつ強力な道具となります。

　前回のゲームでは、「工場−倉庫(一次卸)−商社(二次卸)−酒店(小売店)」というサプライチェーン上でのロジスティクスを考えましたが、今回 はより一般的な輸送・配送のロジスティクスを念頭におき、輸配送ロジスティクスの最適化を考えます。シミュレーション は「もしこのようなやり方で意思決定すればどのような結果が生まれるか」を示してくれますが、「どうしたら一番よく なるか」は示してくれないのが普通です。今回は、どうしたら一番よくできるかを明らかにしてくれる最適化の方法を 体験することにします。とりあげるシナリオは、
などロジスティクスに関係の深いものを中心に挙げています。

郵便輸送におけるパレットの偏在と回送

　郵便の実際の輸送量を調べてみるといくつかの特徴があります。一つの特徴は、通常郵便に関しては、大局的にみたとき、都会 の郵便局から地方の郵便局に流れる郵便の量が、地方から都会に流れる郵便の量より多いということです。これに伴って、輸送 に必要となるトラックやパレットが偏在するという問題が生じます。ここでは、パレットを考えることにします。郵便量の 偏りによって、ほっておくと地方の郵便局のパレットが増え、逆に都会の郵便局のパレットは減り、輸送に支障をきたすおそれ が生じます。そこで、どの郵便局からどの郵便局に空のパレットを送り返せば費用を最小にできるかが問題となります。 日本全体の郵便の流れに関してのデータ（見たい方は、郵便輸送量データファイルを参照してください） もありますが、主要な局だけでも70局を超え、膨大なデータとなるので、ここでは以下の7局からなる小さな郵便ネットワークでの問題を 考えることにします。

　 X Y Z A B C D 送出量計 受取量計 送出−受取
X 　 140 100 70 50 30 60 450 350 100
Y 120 　 250 180 130 160 150 990 740 250
Z 90 270 　 100 70 80 40 650 500 150
A 50 120 40 　 10 50 30 300 480 -180
B 40 90 30 10 　 10 30 210 300 -90
C 30 70 50 70 20 　 90 330 450 -120
D 20 50 30 50 20 120 　 290 400 -110
受取量計 350 740 500 480 300 450 400 3220 3220 0
ネットワーク図
図　郵便ネットワーク（一部の枝のみ表示）

　この問題を解き、輸送費用を最小にする輸送計画を求めたいのですが、そのために有効なツールが、Excelに装備されている「ソルバー」機能です。 まずは、ソルバー機能の使い方を覚えるため、この問題よりも易しい例題を２つ用意しました。 以下の手順に従って、
１．　Excelファイルのダウンロード

　まず、左メニューの「演習資料・レポート表紙」から次の2つのExcelファイルをダウンロードしてください。

（最初に使うのは、数理計画例題のファイルです。問題集のほうは、あとでつかうので、まだダウンロードできません。）

２．　例題を解く

　例題1　生産計画の立案
　大久保工場では，鉄鋼，電力，労働力という3種類のリソースを使って，2種類の製品を生産している． この工場では，いま来週の生産計画を立てようとしている．リソースの許容範囲の中で，利益を最大にする 生産計画を立てるにはどうしたらよいだろうか．各製品の使用リソース量，リソースの許容上限， 製品1個当たりの利益などは以下の表のようである．

　 製品1 製品2 リソース許容上限
鉄鋼使用量 1 2 14
電力使用量 1 1 8
労働力使用量 3 1 18
利益 2 3 　

　例題2　輸送計画の立案
　早稲田工業では、４ヵ所の原料処理場A,B,C,Dで処理された原料を使って、3つの工場X,Y,Zで生産を行っている。 7月の処理場、および工場の生産計画はすでに決まっているが、原料の輸送は危険を伴うため、非常にコストがかさんでしまう。 輸送費用は、輸送量＊輸送距離、すなわち、延輸送距離に比例することが分かっている。各処理場から工場に送ることのできる原料の供給量、 各工場が生産に必要とする原料の必要量が下表のように与えられ、さらに、各処理場から各工場までの距離が下表の数値 （単位は適当に考えること）で与えられたとき、延輸送距離（輸送量×輸送距離の合計）が最小となる輸送計画を求めよ。

　 工場X 工場Y 工場Z 供給量
処理場A 6 1 5 18
処理場B 4 5 6 9
処理場C 3 6 8 12
処理場D 7 2 10 11
需要量 10 25 15 　
３．　定式化

　ソルバー機能を用いるためには、まず、問題をきちんと定式化して、構造をはっきりさせる必要があります。 定式化にあたってのポイントは，
  1. 変数または決定変数(decision variables)の決定　何が制御可能であり，何を決定変数とするか
  2. 目的関数(objective function)の設定　最適化(最大化/最小化)を図る目標が何で，制御可能な変数といかなる関係をもつか
  3. 制約条件(constraints)の設定　問題を制約する条件が何で，それらの制約と制御可能な変数とがどう結びついているか
の3つです．（例題では変数，目的関数，制約条件の決定がおのずと定まってしまうことが多いのですが， 実際の最適化では，問題の境界条件(boundary condition)が明確に与えられておらず，しかも， 何が本当の目的か明らかでないために，定式化の三項目とも簡単に定まらないことが多いです．）
　定式化は，最終的には数式表現されますが，変数，目的関数，制約条件がすべて具体的な意味をもっているので， 数式表現する前に「言葉による定式化」を心がけるとよいでしょう．言葉による定式化は数理モデルを他人に説明するときにも威力を 発揮し，わかりやすい形でさえあれば表現形式にこだわる必要はありません．

　たとえば、例題1の生産計画の立案では、次のような言葉でモデルを表現できます．
　　変数＝各製品の生産数量
　　目的関数＝総利益
　　制約条件＝各リソースの許容上限を満足
　言葉によるモデルを数式モデルに書き表すために，変数，すなわち，各製品の生産数量をx1，x2と定義すると， 目的関数と制約条件を示した定式化は以下のようになります．

定式化

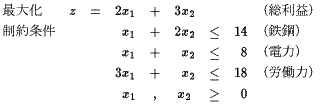
　Excelシート上での表現方法、およびソルバーの使い方は、別紙配布資料を参考にしてください。
４．　数理計画問題集

　数理計画によって最適化する問題が全部で17問あります。演習時間内に、問題1〜8を解いてください(余力がある人は問題9以降も解くこと)。問題16と17は宿題になります。